聯系我們
- 上海耐創測試技術有限公司
- 聯系人:陳工
- 電話:021-39197548
- 郵箱:zhujing@forcechina.com?
- 地址:上海市嘉定區馬陸鎮寶安公路2999弄東方慧谷50號2層

基于矩陣補償方法的串擾修正
文章出處:NaiChuang人氣:發表時間:2021-06-18 14:28:21
基于矩陣補償方法的串擾修正
美國SDI公司 David Schrand
力/力矩傳感器設計用于【沿著定義的軸向,通常標記為X,Y和Z】測量力和力矩。這些力/力矩傳感器由1~6個通道;6通道的力/力矩傳感器包含三個通道的力Fx,Fy,Fz和三個通道的力矩Mx,My,Mz;
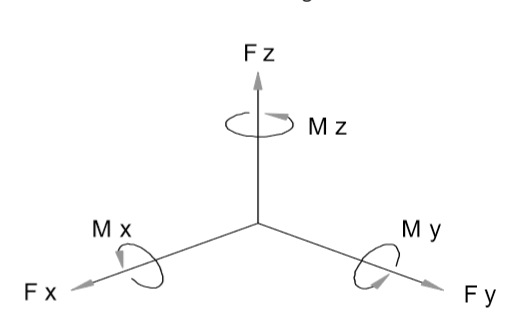
理想狀態是,一個測量軸上的負載將不會在其它任何測量通道上產生輸出。
現實是,沒有任何多軸向傳感器可以做到這種互不干擾;
對于大多數的多通道傳感器而言,這種不需要的輸出,我們稱之為串擾,一般在1%~5%之間;雖然1%~5%的串擾聽起來不多,但是對于有六個通道的力/力矩傳感器而言,每一個通道都會有來自其它五個通道的串擾,這種串擾疊加在一起就可能造成5%~25%的串擾輸出;
基本上,有兩種辦法來減少由多通道之間的串擾帶來的測量誤差:
第一種方法是在傳感器后端加補償電路和對傳感器機械結構進行改良,以求達到減小【非測量軸的外來負載引起的通道輸出】;這種方法雖然有效,但是如果要補償兩個通道以上的外部負載,這種方法是耗時且不切實際的;
第二種是通過數學方法,對各個軸向的負載輸出進行解析校準來得出正確的通道輸出值,這種方法對于任何數量的外部載荷都是有效的,并且可以通過應用“交叉耦合系數”或逆矩陣方法來表征為數學串擾補償。
我們將要講的就是矩陣系數方法。
當負載施加到力傳感器時,與該負載對應的測量通道將響應輸出。然而,如前所述,與施加的負載軸向不一致的其他測量通道也將對該負載做出響應。這是壞消息,好消息是,對于任何給定的負載或負載組合,該響應是可重復的。這意味著通過在校準過程中仔細地應用這些無關的負載,并記錄每個通道輸出響應到這些負載,可以創建傳感器的輸出輪廓。
從這里,可以創建一系列聯立方程來描述力傳感器的串擾性能。通過使用來自傳感器的所有通道的任何一組同時數據來求解該系列方程,可以確定產生該唯一數據集的真實負載條件。該方法的缺點在于,需要加載標定傳感器的所有軸向。這通常不是問題,因為在大多數情況下,我們可以在加載的同時用數據采集設備監測每一個通道的輸出。
OFx = K1 ·Fx
同時,其他五個通道的輸出將被記錄為串擾輸出。現在傳感器的傳遞功能開始形成。
OFx = K1·Fx
OFy = K7·Fx
OFz = K13·Fx
OMx = K19·Fx
OMy = K25·Fx
OMz = K31·Fx
通過這一組方程,可以通過將傳感器輸出除以施加的負載來確定每個軸的傳遞函數(K1,K7等)。
將使用相同的過程來校準傳感器的剩余五個軸,提供剩余的傳遞函數。 使用疊加理論,可以組合產生完全描述傳感器對所有施加載荷的輸出的輸出方程。
OFx = K1·Fx + K2·Fy + K3·Fz + K4·Mx + K5·My + K6·Mz
OFy = K7·Fx + K8·Fy + K9·Fz + K10·Mx + K11·My + K12·Mz
OFz = K13·Fx + K14·Fy + K15·Fz + K16·Mx + K17·My + K18·Mz
OMx = K19·Fx + K20·Fy + K21·Fz + K22·Mx + K23·My + K24·Mz
OMy = K25·Fx + K26·Fy + K27·Fz + K28·Mx + K29·My + K30·Mz
OMz = K31·Fx + K32·Fy + K33·Fz + K34·Mx + K35·My + K36·Mz
這些方程式描述了傳感器在施加的載荷方面的輸出。 然而,在應用中,負載是未知數,輸出是已知的測量量。 利用這六個方程及其六個未知數(載荷Fx-z和Mx-z),可以解決未知載荷;
【逆矩陣方法】
可以通過使用所謂的逆矩陣法來解決上述的一系列方程式。反矩陣理論,我們可以參考線性代數中的逆矩陣求法來取得【K·K-1=E】。實質上,這是一種“反轉”方程式的技術,使得不再像上述那樣將輸出作為負載的函數,所以負載現在是輸出的功能。
用于糾正或補償由于串擾錯誤導致的傳感器輸出的逆矩陣涉及到收集傳感器上的校準數據對外部負載的響應,并使用它構建可用于找到傳感器真實負載條件的矩陣。已經經過徹底校準的多軸傳感器將已經具有提供校準數據的這種串擾矩陣。有關創建此矩陣涉及的步驟的更多信息,請參見附錄B“查找逆矩陣”。
這可能看起來很混亂,但是處理一個非常復雜的問題是一個非常簡單的方法。例如,我們有一個“不太完美”的傳感器。然而,我們確實提供了傳感器提供的串擾矩陣,如下所示。
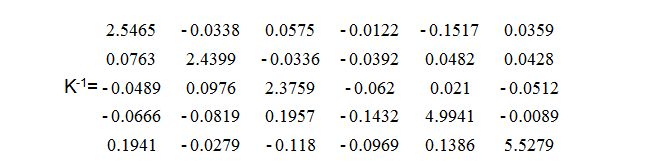
X = K-1·O
使用該逆矩陣,可以計算產生來自傳感器的任何一組同時數據的負載。 我們從逆矩陣K-1和方程式開始:
X = K-1·O
或者展開寫:
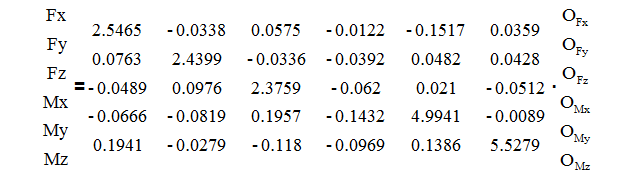
OFx = -1.6510 mV/V OMx = 1.0054 mV/V
OFy = 0.6151 mV/V OMy = 0.8402 mV/V
OFz = 0.2501 mV/V OMz = 0.0067 mV/V
在特定的時間,我們從傳感器獲取以上數據
要找到必須存在的Fx負載來創建這六個輸出,我們將逆矩陣的第一行的元素乘以所記錄的各個輸出,并將它們相加:
Fx = (2.5465 * -1.6510) + (-0.0338 * 0.6151) + … + (0.0359 * 0.0067) = -4.35 lb
類似的,可以通過對逆矩陣的剩余五行執行相同的操作來計算剩余的五個負載,這樣就能得出一個完整傳感器的加載概況;
Fx = -4.35 lb Mx = 5.54 in lb
Fy = 1.37 lb My = 4.11 in lb
Fz = 0.69 lb Mz = -0.31 in lb
在實際使用中,這些計算可以通過數據采集或控制系統實時設置,也可以通過使用電子表格程序在測試完成后對數據進行后處理來完成。 這種技術通常會將串擾減少到傳感器滿量程的0.5%。
美國SDI公司 David Schrand
力/力矩傳感器設計用于【沿著定義的軸向,通常標記為X,Y和Z】測量力和力矩。這些力/力矩傳感器由1~6個通道;6通道的力/力矩傳感器包含三個通道的力Fx,Fy,Fz和三個通道的力矩Mx,My,Mz;

理想狀態是,一個測量軸上的負載將不會在其它任何測量通道上產生輸出。
現實是,沒有任何多軸向傳感器可以做到這種互不干擾;
對于大多數的多通道傳感器而言,這種不需要的輸出,我們稱之為串擾,一般在1%~5%之間;雖然1%~5%的串擾聽起來不多,但是對于有六個通道的力/力矩傳感器而言,每一個通道都會有來自其它五個通道的串擾,這種串擾疊加在一起就可能造成5%~25%的串擾輸出;
基本上,有兩種辦法來減少由多通道之間的串擾帶來的測量誤差:
第一種方法是在傳感器后端加補償電路和對傳感器機械結構進行改良,以求達到減小【非測量軸的外來負載引起的通道輸出】;這種方法雖然有效,但是如果要補償兩個通道以上的外部負載,這種方法是耗時且不切實際的;
第二種是通過數學方法,對各個軸向的負載輸出進行解析校準來得出正確的通道輸出值,這種方法對于任何數量的外部載荷都是有效的,并且可以通過應用“交叉耦合系數”或逆矩陣方法來表征為數學串擾補償。
我們將要講的就是矩陣系數方法。
當負載施加到力傳感器時,與該負載對應的測量通道將響應輸出。然而,如前所述,與施加的負載軸向不一致的其他測量通道也將對該負載做出響應。這是壞消息,好消息是,對于任何給定的負載或負載組合,該響應是可重復的。這意味著通過在校準過程中仔細地應用這些無關的負載,并記錄每個通道輸出響應到這些負載,可以創建傳感器的輸出輪廓。
從這里,可以創建一系列聯立方程來描述力傳感器的串擾性能。通過使用來自傳感器的所有通道的任何一組同時數據來求解該系列方程,可以確定產生該唯一數據集的真實負載條件。該方法的缺點在于,需要加載標定傳感器的所有軸向。這通常不是問題,因為在大多數情況下,我們可以在加載的同時用數據采集設備監測每一個通道的輸出。
OFx = K1 ·Fx
同時,其他五個通道的輸出將被記錄為串擾輸出。現在傳感器的傳遞功能開始形成。
OFx = K1·Fx
OFy = K7·Fx
OFz = K13·Fx
OMx = K19·Fx
OMy = K25·Fx
OMz = K31·Fx
通過這一組方程,可以通過將傳感器輸出除以施加的負載來確定每個軸的傳遞函數(K1,K7等)。
將使用相同的過程來校準傳感器的剩余五個軸,提供剩余的傳遞函數。 使用疊加理論,可以組合產生完全描述傳感器對所有施加載荷的輸出的輸出方程。
OFx = K1·Fx + K2·Fy + K3·Fz + K4·Mx + K5·My + K6·Mz
OFy = K7·Fx + K8·Fy + K9·Fz + K10·Mx + K11·My + K12·Mz
OFz = K13·Fx + K14·Fy + K15·Fz + K16·Mx + K17·My + K18·Mz
OMx = K19·Fx + K20·Fy + K21·Fz + K22·Mx + K23·My + K24·Mz
OMy = K25·Fx + K26·Fy + K27·Fz + K28·Mx + K29·My + K30·Mz
OMz = K31·Fx + K32·Fy + K33·Fz + K34·Mx + K35·My + K36·Mz
這些方程式描述了傳感器在施加的載荷方面的輸出。 然而,在應用中,負載是未知數,輸出是已知的測量量。 利用這六個方程及其六個未知數(載荷Fx-z和Mx-z),可以解決未知載荷;
【逆矩陣方法】
可以通過使用所謂的逆矩陣法來解決上述的一系列方程式。反矩陣理論,我們可以參考線性代數中的逆矩陣求法來取得【K·K-1=E】。實質上,這是一種“反轉”方程式的技術,使得不再像上述那樣將輸出作為負載的函數,所以負載現在是輸出的功能。
用于糾正或補償由于串擾錯誤導致的傳感器輸出的逆矩陣涉及到收集傳感器上的校準數據對外部負載的響應,并使用它構建可用于找到傳感器真實負載條件的矩陣。已經經過徹底校準的多軸傳感器將已經具有提供校準數據的這種串擾矩陣。有關創建此矩陣涉及的步驟的更多信息,請參見附錄B“查找逆矩陣”。
這可能看起來很混亂,但是處理一個非常復雜的問題是一個非常簡單的方法。例如,我們有一個“不太完美”的傳感器。然而,我們確實提供了傳感器提供的串擾矩陣,如下所示。

X = K-1·O
使用該逆矩陣,可以計算產生來自傳感器的任何一組同時數據的負載。 我們從逆矩陣K-1和方程式開始:
X = K-1·O
或者展開寫:

OFx = -1.6510 mV/V OMx = 1.0054 mV/V
OFy = 0.6151 mV/V OMy = 0.8402 mV/V
OFz = 0.2501 mV/V OMz = 0.0067 mV/V
在特定的時間,我們從傳感器獲取以上數據
要找到必須存在的Fx負載來創建這六個輸出,我們將逆矩陣的第一行的元素乘以所記錄的各個輸出,并將它們相加:
Fx = (2.5465 * -1.6510) + (-0.0338 * 0.6151) + … + (0.0359 * 0.0067) = -4.35 lb
類似的,可以通過對逆矩陣的剩余五行執行相同的操作來計算剩余的五個負載,這樣就能得出一個完整傳感器的加載概況;
Fx = -4.35 lb Mx = 5.54 in lb
Fy = 1.37 lb My = 4.11 in lb
Fz = 0.69 lb Mz = -0.31 in lb
在實際使用中,這些計算可以通過數據采集或控制系統實時設置,也可以通過使用電子表格程序在測試完成后對數據進行后處理來完成。 這種技術通常會將串擾減少到傳感器滿量程的0.5%。













 滬公網安備 31011402003414號
滬公網安備 31011402003414號